Minitest::Benchmark: An Introduction
Written: Apr 28, 2015
It’s not old, it’s vintage.
This post was last updated some years ago and hasn’t been updated recently. Be aware that some of the content, tools, and techniques described may not be completely up-to-date.
As more developers have started to use Minitest, the number of resources available for learning about the framework has gradually been growing. We’ve never been short on cheat sheets or references, but as the community has grown, we’ve seen more and more articles focused on specific aspects of the framework being published. That’s good for everyone involved.
One area where there’s still very little information available, though, is Minitest benchmarks. If you’ve looked into the framework at all, you’re probably aware that it allows developers to make assertions about the performance of the code they write. Still, most developers never or rarely use this feature or understand what it does or how to get started. In this first post of a three-part series, I want to explain what Minitest::Benchmark is and how it works in a clear, easy to understand way.
What’s a benchmark good for?
The word benchmark is seriously overloaded within the IT domain, so developers make all kinds of assumptions about what Minitest::Benchmark is and does. Well, at least I did. Before I started digging into it, I’d always assumed that benchmarks were a tool for demonstrating that a given piece of code could be executed within a certain time limit. But think about that for a moment. Pass or fail, what would the absolute performance of a given amount of work within a testing environment tell me about the performance of my application in production? Practically nothing of value. While my definition wasn’t exactly wrong, it wasn’t complete either.
Here’s what I found: a Benchmark in Minitest is a specialized test (actually a subclass of Minitest::Test) that executes the same block of code repeatedly with varied inputs to show the relative performance of the algorithm against increasing demands. It does not assert, for example, that a method or chunk of code will execute within a given duration; rather, it makes predictions about how execution time will change with different inputs and workloads.
In order to clarify what a Benchmark does, we’ll want to understand it as a process with four steps:
- Define a range of inputs.
- Assert the performance of your algorithm.
- Execute the benchmark.
- Check the validity of your assertion.
Let’s break this down further so that we can understand each of these individually.
Step 1: Define a range of inputs.
Each Benchmark needs a range of values that will be fed to the code under test during execution, and this is defined by the bench_range class method. Because it’s the result of a class method, the same range is use for all benchmark tests within the same class. The values in the returned Array must be numeric and should, in most cases, translate into an increasing workload.
The Minitest::Benchmark base class has a default implementation of bench_range that returns an exponential progression of powers of 10 from 1 through 10,000 as shown here:
1
2
irb(main):001:0> Minitest::Benchmark.bench_range
=> [1, 10, 100, 1000, 10000]
You can also override this implementation for each Benchmark subclass, and Minitest provides helper functions for defining both linear and exponential numeric progressions.
1
2
3
4
5
6
7
8
irb(main):002:0> Minitest::Benchmark.bench_linear(0, 50)
=> [0, 10, 20, 30, 40, 50]
irb(main):003:0> Minitest::Benchmark.bench_linear(0, 256, 64)
=> [0, 64, 128, 192, 256]
irb(main):004:0> Minitest::Benchmark.bench_exp(1, 100_000)
=> [1, 10, 100, 1000, 10000, 100000]
irb(main):005:0> Minitest::Benchmark.bench_exp(1, 256, 2)
=> [1, 2, 4, 8, 16, 32, 64, 128, 256]
Step 2: Assert the performance of your algorithm.
At the core of any Benchmark test is an assertion about the performance of your code given an arbitrary amount of work to do. There are five different assertions supported out of the box:
assert_performance_constant- Execution time should remain constant regardless of inputs.assert_performance_linear- Execution time should increase in proportion to workload.assert_performance_logarithmic- Execution time approaches a maximum limit.assert_performance_exponential- Execution time increases exponentially with workload.assert_performance_power- Execution time increases with workload according to a power function relation.
Like any other kind of test, the assertion is essentially a prediction about the way your code should behave (or in this case, perform) given certain inputs. These predictions can be expressed as mathematical formulas which in turn be expressed graphically.
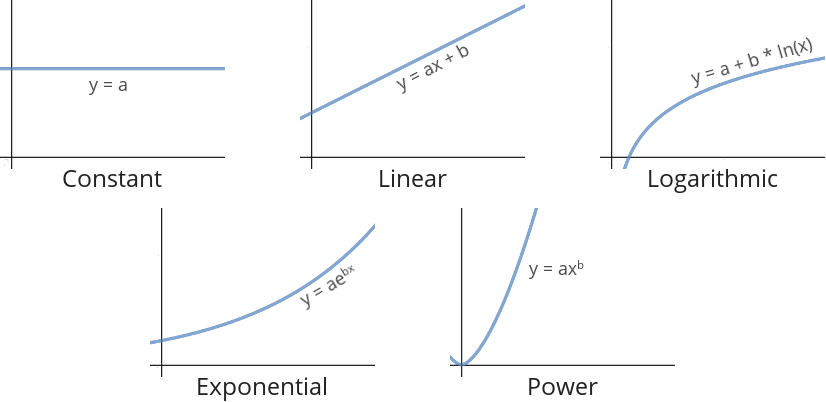
Don’t be intimidated by the math here. It’s actually quite intuitive what each of these things mean:
- x is the numeric input provided to the code under test which represents a certain amount of work to be performed by the code under test.
- y is the predicted execution time resulting from a given input.
- a and b are implementation-specific constants that affect the shape of the curve.
In each case, the assertion method takes two arguments: a threshold value representing how closely the observed execution times match the predictions and a block representing the code under test. We’ll circle back to these shortly.
1
2
3
4
5
6
7
8
9
# test/benchmarks/bench_foo.rb
class BenchFoo < Minitest::Benchmark
def bench_foo
assert_performance_linear 0.99 do |input|
# the code to be benchmarked
# is passed as a block
end
end
end
Step 3: Execute the benchmark.
Minitest runs the benchmark by executing the block once for each input value returned by bench_range. With each execution, it measures the running time and stores it for later comparison.
While your benchmark runs, Minitest will print out the times for each execution of the code under test. The output below is an example from a sample benchmark.
1
2
3
4
5
6
7
8
9
10
11
12
$:> ruby test/benchmarks/bench_types.rb
Run options: --seed 23432
# Running:
bench_fib 0.000020 0.000008 0.000027 0.000447
.bench_snooze 0.463001 0.281439 0.067537 0.459881
.
Finished in 2.825755s, 0.7078 runs/s, 0.7078 assertions/s.
2 runs, 2 assertions, 0 failures, 0 errors, 0 skips
Step 4: Check the validity of your assertion.
Let’s consider what we have by the time we reach the final step of the process:
- An assumption about the general pattern of performance for the algorithm (determined by the assertion type)
- A threshold number describing how closely we expect observed values to match predictions
- The range of inputs used to conduct the benchmark
- Observed execution times for the code under test for each input value in the range
Using all of this and the awesome power of MATH, Minitest can determine the optimal values for the coefficients (recall: a and b from the formulas mentioned above). By “optimal” in this case, we mean the values of a and b such that an equation of the form indicated by the assertion type provides the best representation and prediction of the observed values. That might sound complicated, but essentially, it’s answering the question: what’s the best formula for predicting execution time?
As soon as these values are known, Minitest is also able to quantify how closely our predictions match the real, observed values by computing the coefficient of determination - commonly known as the R-squared value. Without going into the gory technical details, R-squared is just a number between 0.0 and 1.0 that measures how closely the computed function matches the real observed data with a larger value indicating a closer match.
And that brings us back to our test code. Recall that we provided a numeric threshold value when we wrote the original assertion? Well, if the R-squared value is greater than the threshold value we passed to the assertion, it means that the performance fits with the expected model, and our assertion succeeds; if R-squared is less than the threshold though, the assertion fails. So in this way, we haven’t demonstrated that our code is fast or slow, but rather that it performs according to one of these models.
Hopefully that explains a little better about Minitest::Benchmark and what it might be used for. In the next installment, we’ll take a look at how we might be able to apply this knowledge within a realistic use case, and try to understand the value it can provide us.
Additional resources:
- Regression analysis
- Coefficient of determination
- Ruby Benchmarking & Complexity - one of the only detailed technical articles I found on
Minitest::Benchmark